7261. Difficult
path
Alex
drank a lot this night and now when he reached his street, he has completely
lost the sense of direction. Since he can not remember where his house is, he
chooses direction randomly. Moreover, at every crossroads there is a 50% chance
that he will keep going forward or turn around and go back. He so lost his
touch with reality that he can even walk past his own house and not notice it!
Having
passed n blocks, Alex falls asleep
right on the street. When he wakes up, he wonders what were the chances that he
slept near his house? From the crossroads, where he started his way to the
crossroads near his house there are m blocks. Help him.
Input. One line
contains two integers n and m (1
≤ n, m ≤ 1000).
Output.
Print one number - Alex’s chances to fall asleep at the
crossroads right next to his house. Print the result with error not grater than
10-7.
|
Sample
input 1 |
Sample
output 1 |
|
1 1 |
0.5 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
1000 100 |
0.000169397 |
SOLUTION
probability
Algorithm analysis
Let
d be a two dimensional array where d[time][x] is a probability of being at the
point with abscissa x at time time. Let initially (at time t = 0) Alex is located at the point with
the abscissa x = n. Then d[0][n] = 1.
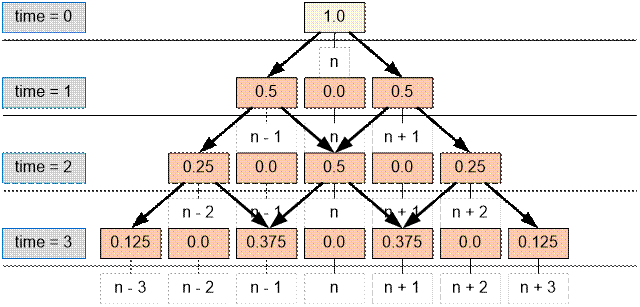
Let’s evaluate d[i][j]
– the probability that Alex at time i
will be at position j. For this Alex
must be located at time i – 1 either
at position j – 1, or at position j + 1. Then at time i he can come from them to position j with probability 50%. So
d[i][j]
= (d[i – 1][j – 1] + d[i – 1][j + 1]) / 2
Let’s consider the
mathematical solution of the problem. We encode the Alex’ path with sequence of
0 and 1. Let 1 means move to the right and 0 means move to the left. Let among n Alex’ steps k steps he did right. Then n
- k steps he did left.
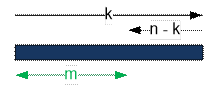
We are interested to find
the probability that Alex moved himself in one of the sides (for example to the
right) m blocks. Then we must have: m
+ n – k = k, where k = (m
+ n) / 2. The number of sequences of
length n with k ones equals to 
. Since Alex made n
movements, he has 2n different
ways to choose the path. So the probability that Alex pass to the right m blocks equals to / 2n, where k = (m + n) / 2. Note that desired probability
equals to 0, if m + n is even. In this case Alex is not able
to reach home (m + n = 2k
is even).
Sample
Let Alex makes n = 3 steps.
If m = 1, then k = (3 + 1) /
2 = 2 and probability equals to 
/ 23 = 3 /
8 = 0.375.
If m = 3, then k = (3 + 3) /
2 = 3 and probability equals to 
/ 23 = 1 /
8 = 0.125.
Let Alex makes n = 4 steps.
If m = 0, then k = (4 + 0) /
2 = 2 and probability equals to 
/ 24 = 6 /
16 = 0.375.
If m = 2, then k = (4 + 2) /
2 = 3 and probability equals to 
/ 24 = 4 /
16 = 0.25.
If m = 4, then k = (4 + 4) /
2 = 4 and probability equals to 
/ 24 = 1 /
16 = 0.0625.
Algorithm realization
We declare the two
dimensional array for calculating the probabilities.
#define MAX
2010
double
d[MAX][MAX];
Read the input data. Initialize the array d.
scanf("%d %d",&n,&m);
memset(d,0,sizeof(d));
d[0][n]
= 1;
Recalculate the probabilities according to given
recurrence relation.
for(i =
1; i <= n; i++)
for(j = n -
i; j <= n + i; j++)
d[i][j] = (d[i-1][j-1] + d[i-1][j+1]) / 2;
Print the answer – the probability that Alex will move
in one of the sides (for example to the right) m blocks and will find his home.
printf("%.9lf\n",d[n][n+m]);
Java
realization
import java.util.*;
public class Main
{
public static void main(String []args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
double d[][] = new double[n+1][2*n+1];
d[0][n] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = n - i; j <= n + i; j++)
{
double a = (j - 1 < 0) ? 0 : d[i-1][j-1];
double b = (j + 1 > 2*n) ? 0 : d[i-1][j+1];
d[i][j] = (a + b) / 2;
// d[i][j] = (d[i-1][j-1] + d[i-1][j+1]) / 2;
}
}
double res = (n + m > 2*n) ? 0 : d[n][n+m];
System.out.println(res);
con.close();
}
}